| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2007-11-17 16:19 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
基本回路のインピーダンス、アドミッタンス 他の参考書ではインピーダンスの説明をするために具体的にR,L,Cが組み合わさった回路について電圧と電流の振幅の比であるインピーダンスを導いているが、著者は説明は省略して公式だけ表にまとめている。
後に演習問題で一部自分で導くというのが出てくるが、その前に自分で基本的なRLC組み合わせ回路についてインピーダンスの公式を導いてみることにする。 インピーダンス|Z|は以下の様に定義される |Z|=Em/Im=|E|/|I| 単位はレジスタンスと同じΩである。 アドミッタンス|Y|はインピーダンスの逆数として定義される。 |Y|=1/|Z|=Im/Em=|I|/|E| 単位はコンダクタンスと同じシーメンスである。 著者はRLCの組み合わせ回路についてのインピーダンスの公式から cos(φ)=R/|Z| sin(φ)=X/|Z| であることを示している。ここでXはリアクタンスである。この式は後にインピーダンスの複素表現を極座標上で表す時の布石である。 cos(φ)は力率である。これを利用して以前に出てきた有効電力の式を書き換えると Pa=|E|*|I|*cos(φ)=|E|*|I|*R/|Z|=|I|^2*R と表される。有効電力はとどのつまり回路中の抵抗で消費される電力そのものである。キャパシタンスやインダクタンス中では電力は蓄えられることはあっても消費されることは無いので当たり前の話だが。 |
| webadm | 投稿日時: 2007-11-17 23:06 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
RL直列回路のインピーダンス、アドミッタンス 最初ではまった。以下の図の様なRL直列回路のインピーダンスの式を導くというのだが。
検索したり、他の参考書を見たりするといろいろ解き方はあるようだ。 (1)一階微分方程式を解いて定常解を得る (2)ラプラス変換を使って楽ちんに微分方程式を解いて定常解を得る (3)RとLに関する電圧と電流のベクトル図を重ね合わせて解く (4)三角関数と微分だけを使って式を操作して解を得る (1)は最も歴史が古いガチンコな解き方。今ならMaximaを使えば一発で微分方程式は解けるが、その解は過渡解と定常解が重ねあわさったものなので複雑、巧妙数式を手で整理すれば過渡解と定常解を分離できるが、('A`)マンドクセ、の一言に尽きる。こないだはまった抵抗ラダー問題程は式は複雑にはならないが。 (2)は微分方程式の解法を知らなくても微分方程式の解が簡単に得ることができるヘビサイドという人が広めた今日ラプラス変換やZ変換と呼ばれるヘビサイド演算子を使って解く方法。公式を憶えれば機械的に解くことができる。これは後に学ぶはず。 (3)後に学ぶベクトル記法を使って電流と電圧を極座標上のベクトルとして描き、抵抗とインダクタンスに生じる電圧降下は90度で直交していることから回路の電圧はそのベクトルの和であることから式を立てて電流と電圧の比からインピーダンスを導くもの。これは単純明快で、微分方程式など使わなくても済む。ただベクトル記法は後に出てくるので今扱うわけにはいかない。本によっては交流回路のしょっぱなからRLC直列回路を題材に最初からベクトル記法で説明して一片に理解させようとはしょっているものもある。これはさすがにIPが高くないと無りだろう。 (4)は途中までは自分でも考えたが最後の詰めではまったケース。もう一冊持っている本「電気回路の基礎 足立修一・森大毅 共著 東京電機大学出版局」は"式変形をくどいぐらいに丁寧に記述したこと"と巻頭に書くほどこだわりのある著者により丁寧な解説と数式の操作の一部始終をはしょることなく記述している。RL直列回路に関しても説明が詳しく式の変形過程も行間を読む必要もない程完璧に記述している。ただわかったのは式の変形に使われている三角関数の合成定理が手持ちの数学公式集には載っていないものだったという点。それを除けば確かに三角関数とその微分だけ知っていれば解けるのは理解できた。ただ、ちょっと('A`)マンドクセ。 とりあえず(1),(4)はやっておかないと先駆者の歩んだ道を追体験しないで先へ進むことになる。 |
| webadm | 投稿日時: 2007-11-20 11:08 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
Re: RL直列回路のインピーダンス、アドミッタンス (1)と(4)の方法をいろいろ自分で考えてみたら、どちらも三角関数の合成定理を理解していないと解けないということがわかって躓いた。3日3晩、"sin,cosわかんねぇ..."と悩んだ。どうやら古い数学の教科書では合成定理を教えていなかったらしい。私が学んだ時もたぶん教わってなかったに違いない。手元の共立出版の「数学公式」にも載っていない。コロナ社の薄っぺらい「数表および公式集」にはしっかり載っていた。直角三角形の辺の関係を知っていれば自明なのだが。工学を志すものにとっては鬼門である。ここで脱落する人も多いに違いない。この次ぎのハードルは複素数と有名なオイラーの定理の理解かな。
今まで学んで来た知識だけを使って解くには(4)が一番とりつきやすい。 基本的にはキルヒホッフの法則を交流に適用するだけなのだけれども。抵抗(R)とインダクタンス(L)が直列に接続され同じ電流i(t)が流れるのだから、抵抗による電圧降下vr(t)とインダクタンスによる電圧降下vl(t)を加えたものは電源電圧に常に等しくなるv(t)と言える。 この時に以下の式が成り立つ。 v(t)=vr(t)+vl(t)=R*i(t)+L*di/dt ここで i(t)=Im*sin(ωt+θ) v(t)=Em*sin(ωt+θ+φ) とすると di/dt=d(Im*sin(ωt+θ)/dt=ω*Im*cos(ωt+θ) なので Em*sin(ωt+θ+φ)=R*Im*sin(ωt+θ)+ω*L*Im*cos(ωt+θ) と書き換えることができる。 ここで Em*sin(ωt+θ+φ)=R*Im*sin(ωt+θ)+ω*L*Im*cos(ωt+θ) に着目するとこれは異なる振幅と位相の同じ周期の正弦波を加えたものが異なる振幅と位相の同じ周期の正弦波になることを示す三角関数の合成定理の式が当てはまることを意味する。 両辺をImで割ると (Em/Im)*sin(ωt+θ+φ)=R*sin(ωt+θ)+ω*L*cos(ωt+θ) ここで |Z|=Em/Im だったのを思い出して置き換えると |Z|*sin(ωt+θ+φ)=R*sin(ωt+θ)+ω*L*cos(ωt+θ) 三角関数の合成定理を使ってこの式の意味を幾何学図で表すと という構図が見えてくる。ここで直角三角形の3辺の関係より |Z|=sqrt(R^2+(ω*L)^2) ということが明らか。また図より tan(φ)=ω*L/R なので φ=arctan(ω*L/R) 電圧が電流よりφだけ進む、逆に言えば電流が電圧よりφだけ遅れる。 最初i(t)の式をsin(ωt+θ+φ)と置いて解いたらはまった。どうやってもφを負として扱わないと幾何学的に関係が成り立たないのである。 ωLを誘導性リアクタンス(XL)で置き換えれば |Z|=sqrt(R^2+XL^2) φ=arctan(XL/R) と表すことができる。 アドミッタンスはインピーダンスの逆数 |Y|=1/|Z|=1/sqrt(R^2+XL^2) ということになる。 試しにグラフで表示してみるとRとLのそれぞれの電圧降下の位相の違いとそれらを合成した電圧の関係がわかる ところで抵抗RとインダクタンスLを直列にしたものをインピーダンスZの負荷で置き換えた場合に等価になるはずだ。 v(t)=|Z|*i(t) Em*sin(ωt+θ+φ)=|Z|*Im*sin(ωt+θ) ただこの関係式はおかしなことになる。両辺をImで割ると (Em/Im)*sin(ωt+θ+φ)=|Z|*sin(ωt+θ) |Z|=Em/Im なので置き換えると |Z|*sin(ωt+θ+φ)=|Z|*sin(ωt+θ) sin(ωt+θ+φ)=sin(ωt+θ) ということになってしまう。 これはどっか間違っているようだ。いずれ納得いく理屈を考えよう。 |
| webadm | 投稿日時: 2007-11-21 11:21 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
Re: RL直列回路のインピーダンス、アドミッタンス RL直列回路の正弦波交流応答に関して微分方程式を解いてみようとしたら途中で見事に填った。
出だしは簡単である。微分方程式はキルヒホッフの法則から R*i(t)+L*di/dt=Em*sin(ωt+θ) これは P*y(x)+Q*y'(x)=F(x) という典型的な一階線形微分方程式である。 これの解き方は公式が既に決まっていてそれを用いても良いのだが、歴史をたどって地道に解いてみよう。 線形方程式は右辺のF(x)を0とした同次方程式もしくは斎次方程式(どちらも変換辞書には入っていない)と呼ばれる微分方程式の解が一般解である R*i(t)+L*di/dt=0 一階の微分方程式の解は指数関数になることがわかっているので、仮にi(t)=exp(λ*t)を解として代入してみる di/dt=(exp(λ*t))'=λ*exp(λ*t) なので R*exp(λ*t)+L*λ*exp(λ*t)=0 exp(λ*t)は共通項なので割ると消える R+L*λ=0 従って λ=-R/L 従って一般解は i(t)=C*exp((-R/L)*t) となる。これはRL直列回路に最初に正弦波交流電源を接続した際の過渡現象に対応する過渡解を構成する。Cは初期条件で決まる積分定数である。 更に右辺をF(x)とおいた非同次方程式もしくは非斎次方程式の解を解くには、同様に以下の仮の解の式を微分方程式に代入する。 i(t)=A*sin(ωt+θ)+B*cos(ωt+θ) di/dt=A*ω*cos(ωt+θ)-B*ω*sin(ωt+θ) とすると R*(A*sin(ωt+θ)+B*cos(ωt+θ))+L*(A*ω*cos(ωt+θ)-B*ω*sin(ωt+θ))=Em*sin(ωt+θ) 左辺を整理すると (R*A-L*B*ω)*sin(ωt+θ)+(R*B+L*A*ω)*cos(ωt+θ)=Em*sin(ωt+θ) これを満たすには (R*A-L*B*ω)=Em (R*B+L*A*ω)=0 を満たすA,Bを連立方程式を解いて求めれば良い (%i4) e1: (R*A-L*B*o)=Em; (%o4) A*R-o*B*L=Em (%i5) e2: (R*B+L*A*o)=0; (%o5) B*R+o*A*L=0 (%i6) solve([e1,e2],[A,B]); (%o6) [[A=(Em*R)/(R^2+o^2*L^2),B=-(Em*o*L)/(R^2+o^2*L^2)]] A=(Em*R)/(R^2+ω^2*L^2) B=-(Em*ω*L)/(R^2+ω^2*L^2) これらを元の式に代入すると i(t)=A*sin(ωt+θ)+B*cos(ωt+θ) =Em*R*sin(ωt+θ)/(R^2+ω^2*L^2)-Em*ω*L*sin(ωt+θ)/(R^2+ω^2*L^2) =Em*(R*sin(ωt+θ)-ω*L*sin(ωt+θ))/(R^2+ω^2*L^2) ここで =Em*(R*sin(ωt+θ)/sqrt(R^2+ω^2*L^2)-ω*L*cos(ωt+θ)/sqrt(R^2+ω^2*L^2))/sqrt(R^2+ω^2*L^2) と書き換えると三角関数の合成定理により sin(φ)=ω*L/sqrt(R^2+ω^2*L^2) cos(φ)=R/sqrt(R^2+ω^2*L^2) tan(φ)=ω*L/R と置くことで i(t)=Em*(cos(φ)*sin(ωt+θ)-sin(φ)*cos(ωt+θ))/sqrt(R^2+ω^2*L^2) 三角関数の加法定理により i(t)=Em*sin(ωt+θ-φ)/sqrt(R^2+ω^2*L^2) ここで i(t)=Im*sin(ωt+θ-φ) とすると Z=Em/Im なのでインピーダンスは |Z|=Em/Im=sqrt(R^2+ω^2*L^2) となる。 従って微分方程式の解は i(t)=C*exp(-R*t/L)+Em*sin(ωt+θ-φ)/|Z| 最初のexpの項はtが十分大きいと0に限りなく近づくので定常状態では i(t)=Em*sin(ωt+θ-φ)/|Z| である。 アドミッタンスはインピーダンスの逆数 |Y|=1/|Z|=1/sqrt(R^2+ω^2*L^2) RL直列回路の正弦波交流応答を微分方程式から導く方法を詳しく説明している参考書はほとんどない。理由は、著者が単に('A`)マンドクセという理由からに違いない。ほとんどの参考書では説明省略、公式だけ示して交流回路の基本終わりとしているものも多い。学校とかでは講義に出席した学生のみ解き方を教わるのかもしれない。そういう意味ではある種電気工学界での秘伝にあたるのかもしれない。 たぶん交流回路の初歩で一番難所なのはこことベクトル記法に切り替わる時かもしれない。もっとも実学的には公式を丸暗記すれば計算とかはそれで十分なのだが。しかし試験とかではしっかりここらへんの理解があるかどうか確かめる問題が出るらしい。その問題を落としても他の問題をすべて正解していれば合格はできるのだろうけど、先駆者の歩んだ道を追体験する上ではここをマスターしないともぐりと言われてもしかたがないかもしれない。 ちなみにMaximaでこの微分方程式は簡単に解ける。 (%i124) i*R+('diff(i,x,1))*L=Em*sin(o*x+s); (%o124) i*R+('diff(i,x,1))*L=Em*sin(o*x+s) (%i125) ode2(%, i, x); (%o125) i=%e^(-(x*R)/L)*((Em*((cos(s)*sin(o*x+2*s)-sin(s)*cos(o*x+2*s)+cos(s)*sin(o*x)+sin(s)*cos(o*x))* L*R+(-o*sin(s)*sin(o*x+2*s)-o*cos(s)*cos(o*x+2*s)+o*sin(s)*sin(o*x)-o*cos(s)*cos(o*x))*L^2)*%e^((x*R)/L))/( L*((2*sin(s)^2+2*cos(s)^2)*R^2+(2*o^2*sin(s)^2+2*o^2*cos(s)^2)*L^2))+%c) (%i126) trigreduce(%); (%o126) i=(%c*R^2)/(R^2*%e^((x*R)/L)+o^2*L^2*%e^((x*R)/L))+(%c*o^2*L^2)/(R^2*%e^((x*R)/L)+o^2*L^2*%e^((x*R)/L))+(Em*sin(o*x+s)*R)/(R^2+o^2*L^2)-(Em*o*cos(o*x+s)*L)/(R^2+o^2*L^2) (%i127) factor(%); (%o127) i=(%e^(-(x*R)/L)*(Em*sin(o*x+s)*R*%e^((x*R)/L)-Em*o*cos(o*x+s)*L*%e^((x*R)/L)+%c*R^2+%c*o^2*L^2))/(R^2+o^2*L^2) ちょっと余計な因数分解がされているが整理して書き直すと i(t)=(Em*sin(ωt+θ)*R-Em*ω*cos(ωt+θ)*L)/(R^2+ω^2*L^2)+%c*exp(-(t*R)/L) ということで最初に手で求めた式と同じものが得られている。これから先はさすがにMaximaも自動的には整理してくれないので同様に手で書き換えれば同じ様に次ぎの結果が得られる。 i(t)=Em*sin(ωt+θ-φ)/sqrt(R^2+ω^2*L^2)+C*exp(-(t*R)/L) この式でt=0,i=0を初期条件とすると積分定数Cは (%i133) solve(C*%e^(-(0*R)/L)+(Em*sin(o*0+s-p))/sqrt(R^2+o^2*L^2)=0,C); (%o133) [C=-(Em*sin(s-p))/sqrt(R^2+o^2*L^2)] C=-(Em*sin(θ-φ))/sqrt(R^2+ω^2*L^2) と解ける。 i(t)=Em*sin(ωt+θ-φ)/sqrt(R^2+ω^2*L^2)-(Em*sin(θ-φ)/sqrt(R^2+ω^2*L^2))*exp(-(t*R)/L) ここで φ=atan(ω*L/sqrt(R^2+ω^2*L^2)) なので 定数Em=1,R=10,L=10,ω=10,θ=0を代入すると i(t)=1*sin(10*t+0-atan(10*10/sqrt(10^2+10^2*10^2)))/sqrt(10^2+10^2*10^2)-(1*sin(0-atan(10*10/sqrt(10^2+10^2*10^2)))/sqrt(10^2+10^2*10^2))*exp(-(t*10)/10) 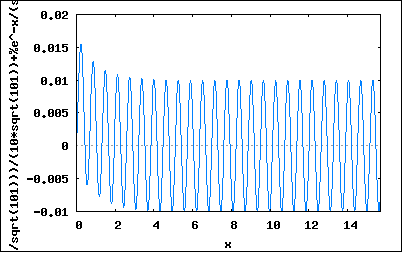 ということで電源をつないだ直後を除いた定常状態では正弦波の波形となっていることがわかる。 微分方程式を解くのはこうした過渡現象を解析する時ぐらいなので学校によっては交流回路の前に過渡現象解析をやるところもある。そうした方が確かに正弦波応答に関しても正しい理解が得られるからだろう。どうしても定常解だけみるとt=0で既に電流が流れているという解になるので狐につままれた気分が抜けないのは確か。本当は過渡解と定常解の合成であることを理解すればそうしたもやもやも晴れる。その後は定常状態だけを扱うという前提でいくので問題ない。 それと交流回路の本流はベクトル記法(複素ベクトル)が使用されるので三角関数が登場する機会は少なくなる。最初からベクトル記法で説明している参考書や学校もあるので、もはや歴史に埋もれた盲腸みたいなものかもしれない。 |
| webadm | 投稿日時: 2007-11-22 6:09 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
Re: RL直列回路のインピーダンス、アドミッタンス RL直列回路で特筆すべき点は、インピーダンスが周波数が上がるにつれて高くなる点である。
インピーダンス中に占める抵抗値の値は変わらないが、インダクタンスによるリアクタンスが周波数が高くなるにつれ増加していく。従って抵抗の両端を出力とすればRL直列回路はローパスフィルターとして機能する。逆にインダクタンスの電圧降下を出力とすればハイパスフィルターとして機能する。 低周波ではよほど大きなインダクタンスか電流を流さない限りほとんど影響が出る程の電圧降下を発生しないので、低周波回路では小さなインダクタンスは無視できる。逆に高周波回路では角速度が大きくなるのでインピーダンス中に占めるリアクタンスの割合が増加するため無視できなくなる。高周波回路の増幅とかでは良くインダクタによって生じた電圧降下をキャパシタか誘導トランスによってAC結合して高周波成分を取りだしているのは当たり前に見られる。もっと高い周波数になるとただの配線が持つインダクタンス成分も無視できなくなる。 ローパスフィルターとして使われるのは高周波をインダクタンスによってブロックもしくはフィルターする用途に使われる。 以下は回路シミュレーターによってローパスフィルターとハイパスフィルターとして機能する様子を示したもの。グラフは横軸が周波数で縦軸が抵抗とインダクタンスのそれぞれの電圧降下を示している。 見ると1.6kHz点で抵抗とインダクタンスの電圧降下が等しくなっているが、単純加算すると電源電圧1vを超えてしまうのは何故だろう。 これはそれぞれの電圧がベクトルの絶対値であること意味する。すなわち電源電圧と抵抗とインダクタンスのそれぞれの電圧を3辺とする直角三角形を形成していることを意味する。RとLの電圧が等しくなった点はその三角形が直角2等辺三角形を形成していることを意味する。直角二等辺三角形の底辺は他の辺のsqrt(2)倍である。底辺以外の2辺の和は、底辺のsqrt(2)倍であるとも言える。実際にRとLの電圧を加えると1.4vぐらいなのでsqrt(2)倍である。 |
| webadm | 投稿日時: 2007-11-22 23:37 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
RC直列回路のインピーダンス、アドミッタンス RL直列回路に続いて今度はRC直列回路。解析の仕方は基本的にはRL直列回路と同じ手法が使えるので結論だけ憶えて先に進むというのが学校の授業では普通だが、やはり先駆者の苦労を追体験するという姿勢からはそういう安直な学習態度は採用できない。
とはいえ、('A`)マンドクセ まずはRL直列回路と同じように簡単な方法から定常状態を解析してみる。 キルヒホッフの法則により抵抗Rの両端の電圧降下とキャパシタンスCの両端の電圧降下の和が電源電圧v(t)と常に等しくなるはずであることから。 v(t)=R*i(t)+(1/C)*Q(t) なる関係が成り立つ。ここでQ(t)はキャパシタンスに蓄えられる電荷量であり電流値i(t)を時間軸上で積分した値である。 Q(t)=Integrate(i(t),t) 従って電流を i(t)=Im*sin(ωt+θ) で表すと (%i2) integrate(Im*sin(o*t+s), t); (%o2) -(Im*cos(o*t+s))/o Q(t)=Integral(Im*sin(ωt+θ),t)=-(1/ω)*cos(ωt+θ) となり先の方程式は v(t)=R*Im*sin(ωt+θ)-(1/ω*C)*Im*cos(ωt+θ) =Im*(R*sin(ωt+θ)-(1/ω*C)*cos(ωt+θ)) ここで |Z|=Em/Im なので Im=Em/|Z| を代入すると v(t)=(Em/|Z|)*(R*sin(ωt+θ)-(1/ω*C)*cos(ωt+θ)) =Em*((R/|Z|)*sin(ωt+θ)-((1/ω*C)/Z)*cos(ωt+θ)) ここで sin(φ)=(1/ω*C)/|Z| cos(φ)=R/|Z| tan(φ)=(1/ω*C)/R なので 式をそれぞれ置き換えると v(t)=Em*(cos(φ)*sin(ωt+θ)-sin(φ)*cos(ωt+θ)) 三角関数の加法定理により v(t)=Em*sin(ωt+θ-φ)=Im*|Z|*sin(ωt+θ-φ) となり電流の位相がφだけ進んでいることを意味する。 この式の関係の意味を幾何学的に表すと 直角三角形の辺の関係からインピーダンスは |Z|=sqrt(R^2+(1/ω*C)^2) アドミッタンスはインピーダンスの逆数 |Y|=1/sqrt(R^2+(1/ω*C)^2) 図形や式から見てとれるようにRC直列回路は位相の向きがRL直列回路と正反対である。周波数が高くなるにつれてインピーダンスは小さくなるのもRL直列回路とは正反対である。 RC直列回路は角速度ω=0(直流)に対してはインピーダンスは∞となり定常状態では電流は流れない。理論的には角速度が高くなるにつれリアクタンスが小さくなり、インピーダンス値は抵抗値に限りなく近づく。現実のRC回路では配線インダクタンス成分が直列に入っているので周波数が高くなるにつれ配線による誘導性リアクタンスの増加が無視できなくなる。 RC直列回路は電源を入力としてキャパシタンスの両端の電圧を出力とするとローパスフィルターとして機能する。逆に抵抗の両端の電圧を出力とするとハイパスフィルターとして機能する。これもRL直列回路とはまったく正反対である。 |
| webadm | 投稿日時: 2007-11-23 6:53 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
Re: RC直列回路のインピーダンス、アドミッタンス 今度は微分方程式を解いてみよう。
回路よりキルヒホッフの定理から R*i(t)+(1/C)*Q(t)=v(t) ここで v(t)=Em*sin(ωt+θ) とすると。 R*i(t)+(1/C)*Q(t)=Em*sin(ωt+θ) しかしこれだとi(t)とQ(t)の両方を解かなければならなくなる。 Q(t)はi(t)のtに関する積分なのでこの式は積分方程式になってしまう。 積分方程式は微分方程式よりマイナーな古典的な数学であり解法も知られている。解が連続である場合には式を微分して得られた微分方程式の解が積分方程式の解であるという定理を利用する方法がある。 もうひとつはi(t)はQ(t)の導関数であることから、方程式をQ(t)に関する微分方程式に書き直してQ(t)の解を求め、それを微分してi(t)を導くという方法。 どちらでも良いが、前者のアプローチで解いてみることにする。 先の方程式をtで両辺を微分すると R*di/dt+(1/C)*i(t)=Em*ω*cos(ωt+θ) これで微分方程式らしくなった。 最初に右辺を0とした以下の同次方程式の解(過渡解)を求める。 R*di/dt+(1/C)*i(t)=0 i(t)=exp(λ*t)と仮定して代入すると R*λ*exp(λ*t)+(1/C)*exp(λ*t)=0 両辺をexp(λ*t)で割って特性方程式 R*λ+(1/C)=0 を得る。これからλは λ=-1/(R*C) すなわち同次方程式の一般解は i(t)=K*exp(-t/(R*C)) ということになる。 続いて右辺をEm*sin(ωt+θ)と置いた非同次方程式の解を解くために仮に解が正弦波の合成から成ることが予想されるので i(t)=A*sin(ωt+θ)+B*cos(ωt+θ) と置いて。方程式に代入すると di/dt=A*ω*cos(ωt+θ)-B*ω*sin(ωt+θ) なので R*(A*ω*cos(ωt+θ)-B*ω*sin(ωt+θ))+(1/C)*(A*sin(ωt+θ)+B*cos(ωt+θ))=Em*ω*cos(ωt+θ) 整理すると (R*A*ω+(1/C)*B)*cos(ωt+θ)+((1/C)*A-R*B*ω)*sin(ωt+θ)=Em*ω*cos(ωt+θ) 従って (R*A*ω+(1/C)*B)=Em*ω ((1/C)*A-R*B*ω)=0 を満たすA,Bを連立方程式として解いて求めれば良い (%i4) solve([(R*A*o+(1/C)*B)=Em*o,((1/C)*A-R*B*o)=0],[A,B]); (%o4) [[A=(Em*o^2*C^2*R)/(o^2*C^2*R^2+1),B=(Em*o*C)/(o^2*C^2*R^2+1)]] 整理すると A=(Em*ω^2*C^2*R)/(ω^2*C^2*R^2+1) =(Em*R)/((ω^2*C^2*R^2+1)*(1/ω^2*C^2)) =(Em*R)/(R^2+(1/ω*C)^2) B=(Em*ω*C)/(ω^2*C^2*R^2+1) =(Em*(1/ω*C))/((ω^2*C^2*R^2+1)*(1/ω^2*C^2)) =(Em*(1/ω*C))/(R^2*(1/ω*C)^2) 従って i(t)=(Em*R)*sin(ωt+θ)/(R^2+(1/ω*C)^2)+(Em*(1/ω*C))*cos(ωt+θ)/(R^2+(1/ω*C)^2) =(Em/sqrt(R^2+(1/ω*C)^2)*((R/sqrt(R^2+(1/ω*C)))*sin(ωt+θ)+((1/ω*C)/sqrt(R^2+(1/ω*C)^2))*cos(ωt+θ)) ここで sin(φ)=(1/ω*C)/sqrt(R^2+(1/ω*C)^2) cos(φ)=R/sqrt(R^2+(1/ω*C)^2) tan(φ)=(1/ω*C)/R とすると i(t)=(Em/sqrt(R^2+(1/ω*C)^2)*(cos(φ)*sin(ωt+θ)+sin(φ)*cos(ωt+θ)) 三角関数の加法定理により i(t)=(Em/sqrt(R^2+(1/ω*C)^2)*sin(ωt+θ+φ) ということで電流が電圧よりもφだけ位相が進むことを示している。 |Z|=Em/Im であることから i(t)=(Em/|Z|)*sin(ωt+θ+φ) ここで直角三角形の辺の関係からインピーダンスは |Z|=sqrt(R^2+(1/ω*C)^2) となりアドミッタンスはその逆数 |Y|=1/sqrt(R^2+(1/ω*C)^2) 従って微分方程式の一般解は i(t)=K*exp(-t/(R*C))+(Em/|Z|)*sin(ωt+θ+φ) ということになる。 ここで φ=atan((1/ω*C)/R) である。 t=0,i=0の初期条件を与えて積分定数Kを解くと (%i5) solve(K*exp(-0/(R*C))+(Em/Z)*sin(o*0+s+p)=0,K); (%o5) [K=-(Em*sin(s+p))/Z] K=-(Em*sin(θ+φ))/|Z| 従って i(t)=-(Em*sin(θ+φ)/|Z|)*exp(-t/(R*C))+(Em/|Z|)*sin(ωt+θ+φ) ここでR=10,C=10^-1,Em=1,θ=0,ω=10とすると i(t)=-(1*sin(0+atan(1/(10*10^-1*10)))/sqrt(10^2+(1/10*10^-1)^2))*exp(-t/(10*10^-1))+(1/sqrt(10^2+(1/10*10^-1)^2))*sin(10*t+0+atan(1/(10*10^-1*10))); これをプロットしてみると 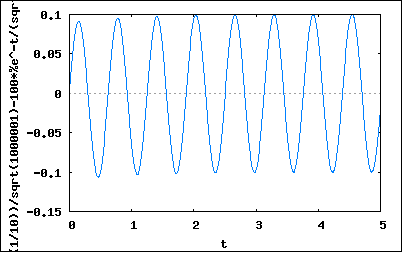 これも電源接続直後の過渡期を除いては安定した正弦波波形となっていることがわかる。 |
| webadm | 投稿日時: 2007-11-23 9:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
Re: RLC直列回路のインピーダンス、アドミッタンス 過渡解も含めて微分方程式(積分方程式)を解こうと試みたら填った。
R*i(t)+L*di/dt+(1/C)*∫i(t)=Em*sin(ωt+θ) なのだがこれを微分すると R*di/dt+L*d^2i/d^2t+(1/C)*i(t)=Em*ω*cos(ωt+θ) となりi(t)に関する二階の微分方程式となる。 しかしこれを解こうとするとはまる。どうりでどの参考書にも書いてないわけだ。 後にRLC直列回路に正弦波交流を加えた時の過渡現象を解析する際に扱う。RL直列回路やRC直列回路は今までそれと知らずに解析してきたがいずれも一階の微分方程式を解くだけの簡単なものだったがこれは違う。 過渡解は複雑になりそうだが定常状態の式は同じになるはずなのでそれを手がかりに解くしかない。 要継続研究。 |
| webadm | 投稿日時: 2007-11-24 1:56 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
LC直列回路のインピーダンス、アドミッタンス どの参考書にもLC直列回路のインピーダンスを求める記述は無い。
何故だろう。 L*di/dt+(1/C)*∫i(t)=v(t) というキルヒホッフの法則は成り立つはずである。 いつもの通り i(t)=Im*sin(ωt+θ) di/dt=Im*ω*cos(ωt+θ) ∫i(t)=-Im*cos(ωt+θ)/ω と仮定して代入すると L*Im*ω*cos(ωt+θ)-(1/C)*Im*cos(ωt+θ)/ω =Im*(ω*L-(1/ω*C))*cos(ωt+θ) Z=Em/Im なので Im=Em/Z を代入すると v(t)=(Em/Z)*(ω*L-(1/ω*C))*cos(ωt+θ) どうもおかしい。 ω*L=1/ω*C の条件では電圧降下が発生しないということを示している。 微分方程式から電流を解析してみよう L*di/dt+(1/C)*∫i(t)=v(t) これを微分して L*di^2/dt^2+(1/C)*i(t)=dv/dt v(t)=Em*sin(ωt+θ) dv/dt=Em*ω*cos(ωt+θ) とすると L*di^2/dt^2+(1/C)*i(t)=Em*ω*cos(ωt+θ) 同次方程式 L*di^2/dt^2+(1/C)*i(t)=0 の特性方程式 L*x^2+(1/C)=0 これの根は (%i9) solve(L*x^2+(1/C)=0,x); (%o9) [x=-1/sqrt(-C*L),x=1/sqrt(-C*L)] ぬお、平方根の中が負だ。虚数表示に直すと x=±j/sqrt(C*L) ということになり、同次方程式の一般解は i(t)=K1*exp(j*t/sqrt(C*L)+K2*exp(-j*t/sqrt(C*L) ということになる。これはよく見るとオイラーの定理とDe Moivreの定理 exp(±jnx)=(cos(x)±j*sin(x))^n =cos(n*x)±k*sin(n*x) によって書き換えると i(t)=K1*(cos(t/sqrt(C*L))+j*sin(t/sqrt(C*L)))+K2*(cos(t/sqrt(C*L))-j*sin(t/sqrt(C*L))) =(K1+K2)*cos(t/sqrt(C*L))+(K1-K2)*j*sin(t/sqrt(C*L)) ここで K1+K2=C j*(K1-K2)=D ω0=1/sqrt(C*L) とすると i(t)=C*cos(ω0*t)+D*sin(ω0*t) また Z=sqrt(C^2+D^2) sin(φ)=C/Z cos(φ)=D/Z tan(φ)=C/D と置くと i(t)=Z*((C/Z)*cos(ω0*t)+(D/Z)*sin(ω0*t)) =Z*(sin(φ)*cos(ω0*t)+cos(φ)*sin(ω0*t)) =Z*sin(ω0*t+φ) と表すことができる。 明らかにω0を角速度とする自由振動関数がとなることは確か。抵抗を含まないので計算上では直流電源を印可するだけで勝手に減衰しない正弦波振動を始めることを意味する。これは力学でも学ぶ、摩擦の無い空間で一端を天井に固定したバネのもう一端に重りをつないだ場合にバネが振動し始めるのと同じ現象である。これらの回路要素に正弦波交流電源を印可すると、その応答と相まって単純な正弦波ではないもっと複雑な波形の電流が流れることが予想される。共振周波数ω0と一致する正弦波交流電源が印可された際には∞に大きな電流が流れることにも。共振現象は機械振動とかでは時にわずかなエネルギーで予想外に大きな力を発生させ部品そのものを破壊することもある。例えば指先一本の力を与え続けるだけで大きな重量の釣り鐘を大きく揺らすことさえ出来るのもその一例である。 回路シミュレーターで共振周波数にほぼ等しい正弦波交流電源をLC直列回路に印可した時の電流と電圧の波形。電流が3A以上も流れているのがわかる。現実の回路でこの様になればコンデンサは発熱しコイルは溶断してもおかしくない。 現実の回路ではL及びCどちらも内部抵抗を含むことから抵抗を含まない回路を解析しても意味が無い。LC回路を扱う場合にもRをなんらかの形で含むことで現実を近似したモデルとすることが可能になる。これで正弦波交流の初歩でRを含まない回路を扱わない理由の一端がわかった気がする。 LCを直列にした回路要素を用いると特定の周波数でインピーダンスが0となる共振特性を持つことから、様々な電子回路への応用がなされている。 これは共振回路や過渡現象を扱う後の機会に取り組む課題としよう。 とりあえず並列回路の正弦波交流応答に関して先に学ぶことに。 |
| webadm | 投稿日時: 2007-11-24 6:40 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3110 |
RL直列回路とRC直列回路の別の用途 既にRL直列回路とRC直列回路は共にハイパスフィルター、ローパスフィルターの両方の電子回路用途に使えることを示したが、別の見方では積分回路と微分回路として電子回路でよく使用される。
それ以外にハイパスフィルターは微分回路として、ローパスフィルターは積分回路として機能することが知られている。 RL直列回路のハイパスフィルターはLの電圧降下を出力とするので Vout=L*di/dt Vin=R*i(t)+L*di/dt 両辺を微分すると dVin/dt=R*di/dt+L*di^2/dt^2=(R/L)*Vout+dVout/dt 従って Vout=(R/L)*dVin/dt-(L/R)*dVout/dt となる。 R>>Lなら Vout≒(R/L)*dVin/dt 入力を微分したものが出力される RL直列回路でRの電圧降下を出力とするとローパスフィルターであると同時に Vout=R*i(t) Vin=R*i(t)+L*di/dt 積分すると ∫Vin=R*∫i(t)+L*i(t)=R*∫i(t)+(L/R)*Vout Vout=(R/L)*∫Vin-(R^2/L)*∫i(t) R<<Lの場合 Vout≒(R/L)*∫Vin となって入力を積分する回路になる RC直列回路のCの電圧降下を出力とするとローパスフィルターであると同時に Vout=(1/C)*∫i(t) Vin=R*i(t)+(1/C)*∫i(t) 積分すると ∫Vin=R*∫i(t)+(1/C)*∫∫i(t)=C*R*Vout+(1/C)*∫∫i(t) ∴Vout=(1/C*R)*∫Vin-(1/(C^2*R)*∫∫i(t) C>>Rの時 Vout≒(1/C*R)*∫Vin 故に入力を積分する回路となる。 同様にRC直列回路のRの電圧降下を出力とした場合、ハイパスフィルターとなると共に Vout=R*i(t) Vin=R*i(t)+(1/C)*∫i(t) 微分すると dVin/dt=R*di/dt+(1/C)*i(t)=R*di/dt+(1/(C*R))*Vout ∴Vout=(C*R)*dVin/dt-(C*R^2)*di/dt R<<Cの時 Vout≒(C*R)*dVin/dt 故に入力を微分する回路となる。 これらの電子回路素子の応用理論は電気回路ではなく電子回路で専門的に扱うので交流理論では扱わない。 いろいろこの先勉強する必要がありそう。 電子回路では電気的な理論をあまり知らなくても出来合の回路をまねすれば実学的に出来てしまうのだが、自分で考えようとするとやはり電気回路の基礎知識が不可欠となる。 |
| (1) 2 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

